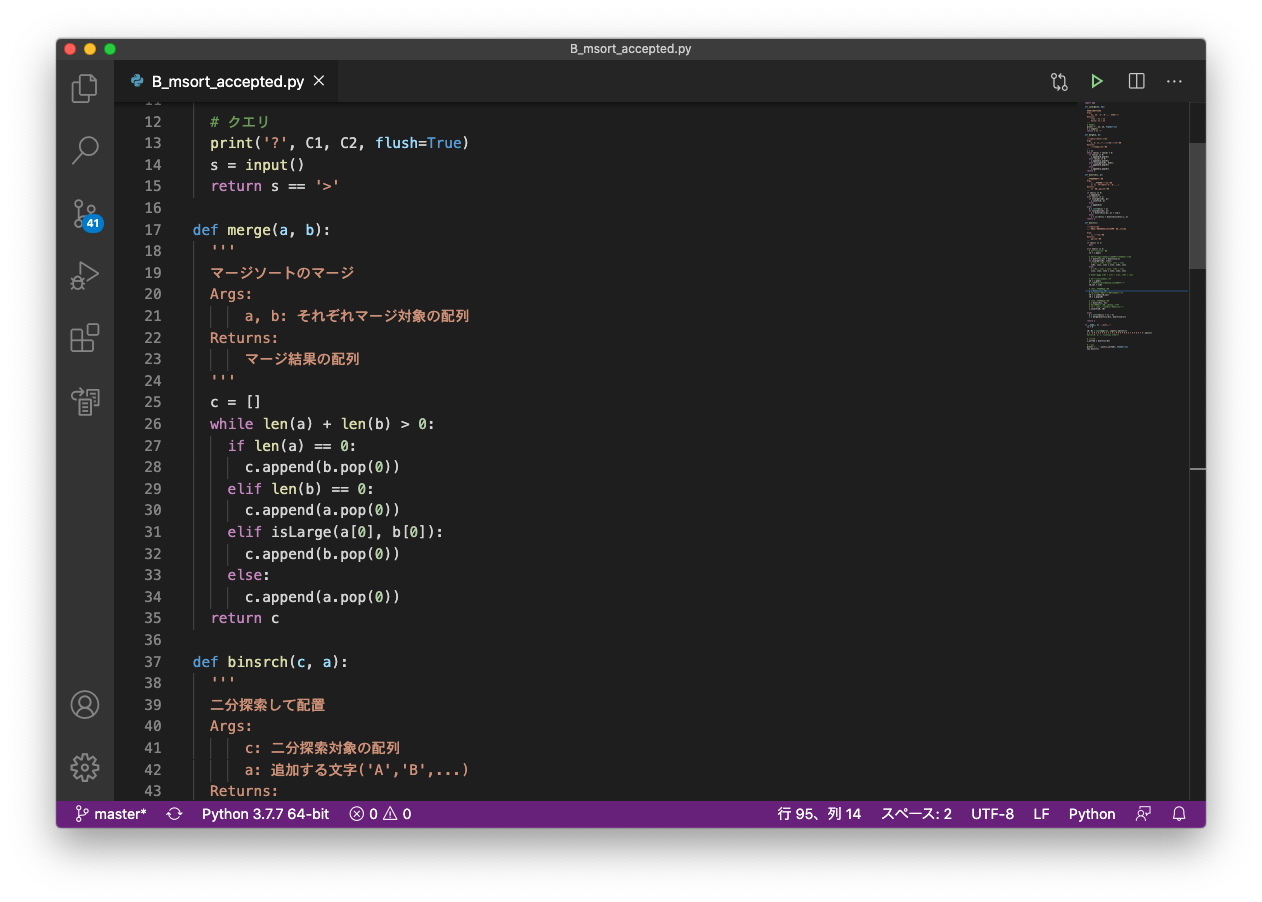
【ソート問題】5個を7回で並び替える問題(B – Interactive Sorting)を解いてみた！ (Python編)

前回、AtCoderの B – Interactive Sortingの問題（5個のデータを7回以内で並び替えるという超難問）を解くことができました！

詳細はこちらの記事です。言語はCで書きました。

【ソート問題】5個を7回で並び替える問題(B – Interactive Sorting)を解いてみた！

先日から、AtCoderの B – Interactive Sortingに挑戦中です。 5個のデータを7回で並び替えるソート問題なのですが、私のような素人には超難問でした。(^^;; マージソートなどのアルゴリズムを当てはめてみても、比較...

今回、お勉強を兼ねて、Pythonに移植してみました。
配列操作がしやすいこともあり、割とスッキリ(自分調べ)したコードになりました!

なお、C言語版は試行錯誤の末、同じクエリを複数回行わないようにキャッシュを作ったりしていましたが、今回はそれは外しました。その代わりに、最後の二分探索を行う際、4個のうち1個(比較済みのc[0])を一時的に取り出して、後から再度追加しています。

ソースコードはGitHubにも置いてありますが、こちらにも貼っておきます。

import sys

def isLarge(C1, C2):
  '''
  クエリして比較
  Args:
      C1, C2: 'A','B',... 比較対象
  Returns:
      True : C1 > C2
      False: C1 < C2
  '''
  # クエリ
  print('?', C1, C2, flush=True)
  s = input()
  return s == '>'

def merge(a, b):
  '''
  マージソートのマージ
  Args:
      a, b: それぞれマージ対象の配列
  Returns:
      マージ結果の配列
  '''
  c = []
  while len(a) + len(b) > 0:
    if len(a) == 0:
      c.append(b.pop(0))
    elif len(b) == 0:
      c.append(a.pop(0))
    elif isLarge(a[0], b[0]):
      c.append(b.pop(0))
    else:
      c.append(a.pop(0))
  return c

def binsrch(c, a):
  '''
  二分探索して配置
  Args:
      c: 二分探索対象の配列
      a: 追加する文字('A','B',...)
  Returns:
      追加した結果の配列
  '''
  if len(c) == 0:
    c.append(a)
  elif len(c) == 1:
    if isLarge(c[0], a):
      c.insert(0, a)
    else:
      c.append(a)
  else:
    m = int(len(c) / 2)
    if isLarge(c[m], a):
      c = binsrch(c[:m], a) + c[m:]
    else:
      c = c[:(m+1)] + binsrch(c[(m+1):], a)
  return c

def msort(c):
  '''
  マージソート
  ただし、配列サイズが5のときだけ独自論理

  Args:
      c: 対象の配列
  Returns:
      結果の配列
  '''
  if len(c) == 1:
    pass

  elif len(c) == 5:
    # 末尾(c[4])を退避
    c4 = c.pop()

    # 残り4個で2個ずつソートして部分的にマージ
    c = msort(c[:2]) + msort(c[2:])
    if isLarge(c[0], c[2]):
      # c[2] < c[0] < c[1], c[2] < c[3]
      c[0], c[1], c[2] = c[2], c[0], c[1]
    else:
      # c[0] < c[2] < c[3], c[0] < c[1]
      c[1], c[2], c[3] = c[2], c[3], c[1]

    # ここまでで c[0] < c[1] < c[2], c[0] < c[3]

    # 末尾(c[3])を取り出す
    c3 = c.pop()
    # 現時点のc[0]の値をc0_valとしてメモ
    c0_val = c[0]

    # c4を二分探索で配置
    c = binsrch(c, c4)
    # c0_valの位置をメモして、取り出す
    n0 = c.index(c0_val)
    c0 = c.pop(n0)

    # c3を二分探索で配置
    c = binsrch(c, c3)
    # さっき取り出したc0を入れ直す
    # c0 < c3のため、n0の位置はそのまま
    c.insert(n0, c0)

  else:
    m = int((len(c) + 1) / 2)
    c = merge(msort(c[:m]), msort(c[m:]))

  return c

if __name__ == '__main__':
  rc = 0

  [N, Q] = list(map(int, input().split()))
  c = 'A B C D E F G H I J K L M N O P Q R S T U V W X Y Z'.split()
  #print(N, Q, c, file=sys.stderr)

  # ソート
  c_sorted = msort(c[:N])

  # ! ans
  print('!', ''.join(c_sorted), flush=True)
  sys.exit(rc)

処理内容は、C言語のものと同様なので、詳細はそちらの記事を参照願います。

AtCoderに提出した結果がこちらです。

さすがに処理速度などはCより劣りますが、制限時間内なので全く問題ないですね。