【ソート問題】5個を7回で並び替える問題(B – Interactive Sorting)を解いてみた！

プログラミング
スポンサーリンク

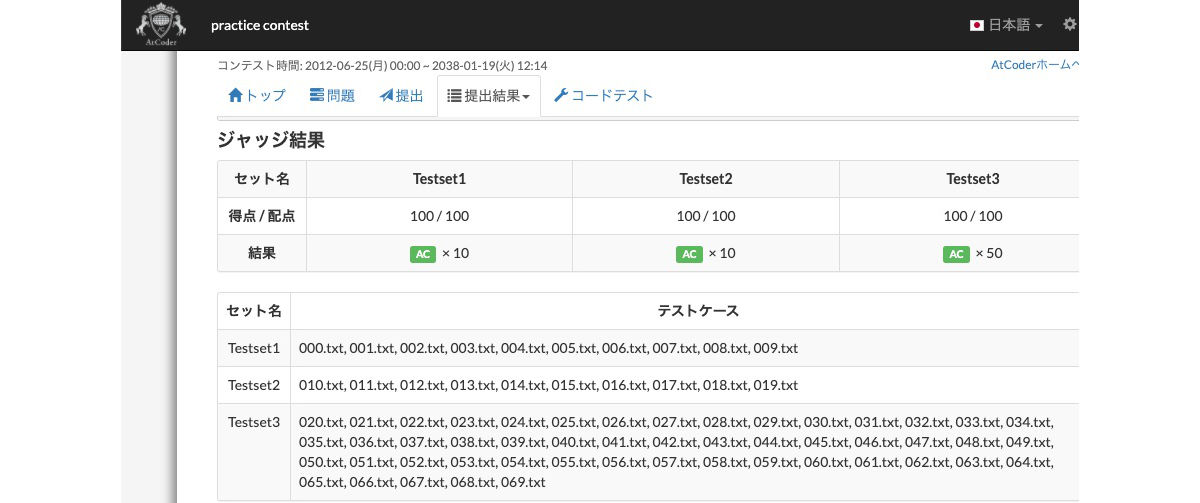
先日から、AtCoderの B – Interactive Sortingに挑戦中です。
5個のデータを7回で並び替えるソート問題なのですが、私のような素人には超難問でした。(^^;;

マージソートなどのアルゴリズムを当てはめてみても、比較回数を7回に収めることができません。そのため、↓こちらの記事のツールを使って試行錯誤しました。。

双方向パイプを使ってAtCoderのインタラクティブ問題を実験してみた！
先日から、競技プログラミング「AtCoder」に挑戦しています！ ↓こちらの記事でも書きましたが、B – Interactive Sortingがなかなか解けません。(^^;; 「5個を7回で並び替える」のが難しいです。。 ソートの方式を何...
picomikan.net
2020.10.25

そして、この度、ついに全てのパターンで7回に収めることに成功しました！

こちらが、AtCoderに提出した結果です。

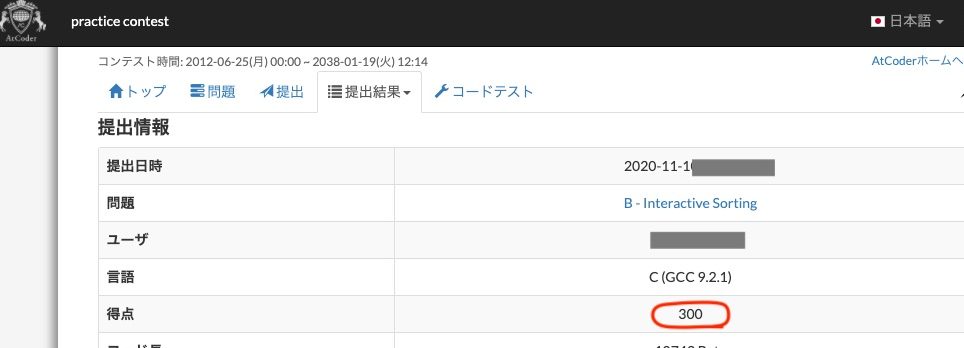
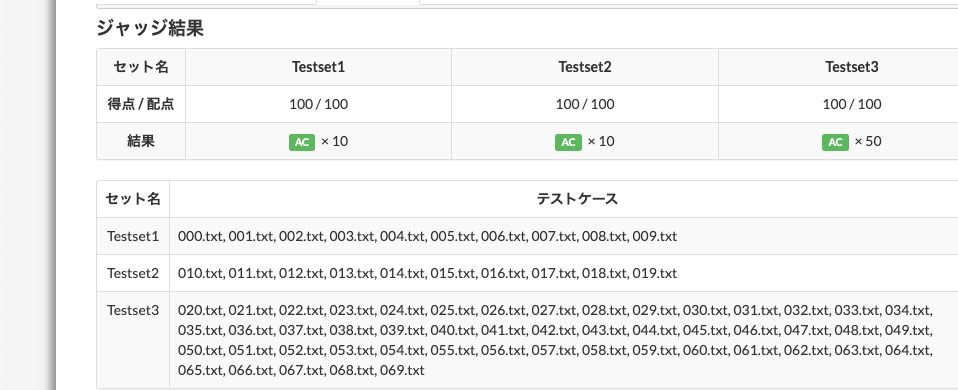
今回は、そのソート方法について説明します。

スポンサーリンク

マージソート(3:2)

手順

はじめに、単純なマージソートの手順で試してみます。

ツール B_question.pyの、5番目のテストサンプル(期待結果：昇順でABEDC)のを使ってテストした結果はこちらの通りです。

$ python ./B_question.py 5  < aaa | ./msort > aaa
B_question: Q No.5 Exp:ABEDC
B_question: Query 1: A < B
B_question: Query 2: A < C
B_question: Query 3: B < C
B_question: Query 4: D > E
B_question: Query 5: A < E
B_question: Query 6: B < E
B_question: Query 7: C > E
B_question: Query 8: C > D
B_question: Ans ABEDC
B_question: Query count over... count= 8

たしかに、比較(クエリ)の回数は7回を超過してしまいます。

処理内容を詳しくみると、以下のとおりです。

  1. ABCDE を 前半ABCと後半DEに分割
  2. 再帰的にABCを前半ABと後半Cに分割
  3. AとBを比較して、A<Bと判明。(比較回数: 計1)
  4. Cとマージするとき、A<C, B<Cが判明。(計3)
  5. DとEを比較して、E<Dが判明。(計4)
  6. ABCとEDをマージ。まず、Eの場所を探す。A<E, B<E, E<Cが判明。(計7)
  7. Eより後方にDの位置を探す。D<Cが判明。(計8)
  8. ABEDCの順番が判明。

この結果をベースに、「7回でソート可能」という事実をもとに、冗長なところを改善していきます。

二分探索も組み合わせてみる

上の手順を後ろから順に見ていくと、まず、手順6.でEをマージする際に、ABCの3つと比較している点が冗長に見えます。ABCは既にソート済みなので、頭から全部と比較してしまうのはもったいないです。

二分探索により、初めに真ん中のBと比較し、その結果に応じてA or Cと比較すれば、2回の比較で済みます！ 修正したものでテストした結果はこちらの通りです。

$ python ./B_question.py 5  < aaa | ./msort_1 > aaa
B_question: Q No.5 Exp:ABEDC
B_question: Query 1: A < B
B_question: Query 2: A < C
B_question: Query 3: B < C
B_question: Query 4: D > E
B_question: Query 5: B < E
B_question: Query 6: C > E
B_question: Query 7: C > D
B_question: Ans ABEDC
B_question: Accepted !!  (count=7)

少なくともこのケースは7回に収まりました。

二分探索でもNGのケース

上の対応後も7回を超過するケースもあります。
例えば、EABCD(33番目のテストサンプル)で実行した場合です。

$ python ./B_question.py 33  < aaa | ./msort_1 > aaa
B_question: Q.33 Exp:EABCD
B_question: Query 1: A < B
B_question: Query 2: A < C
B_question: Query 3: B < C
B_question: Query 4: D > E

ここまでは全く同じ手順です。この時点で、A<B<C と E<D が判明しています。

B_question: Query 5: B > E
B_question: Query 6: A > E
B_question: Query 7: B < D
B_question: Query 8: C < D
B_question: Ans EABCD
B_question: Query count over... count= 8

その後、EとDを二分探索でマージしていますが、2回ずつかかってしまっています。

再び冗長な処理を探してみます。
手順4.で E < Dと判明していますが、それより後方の二分探索処理ではその情報はほぼ使っていないように見えます。

ただ、手順4.(後半2個のソート)そのものを無くしても、最後にABCDにEを追加する際、3回も比較してしまい、やはり超過してしまいました。
実行結果は以下です。

$ python ./B_question.py 33  < aaa | ./msort_2 > aaa
B_question: Q.33 Exp:EABCD
B_question: Query 1: A < B
B_question: Query 2: A < C
B_question: Query 3: B < C
B_question: Query 4: B < D
B_question: Query 5: C < D
B_question: Query 6: C > E
B_question: Query 7: B > E
B_question: Query 8: A > E
B_question: Ans EABCD
B_question: Query count over... count= 8

ここでちょっと手詰まりとなりました。。

感覚的に改善の余地がありそうなところは以下でした。

  • 最初に前半3個の中でソートして順序を決定してしまっているが、早すぎるのではないか？
    特にABEDCのテストケースの場合、Cは最大にもかかわらず、早々とABと比較している。必要になったときで良い？
  • マージソートは、半分の半分の・・・と細分化してソートしてマージしていくが、3個を2個と1個に分けても効率悪い？
スポンサーリンク

マージソート(4:1)

手順

少し方向性を変えて、マージソートの分割の仕方を変えてみました。
前述の通り、3個のところが効率が悪そうなので、5個を分割するとき、4個と1個に分けてみます。

はじめに、ABECDのテストケースです。

$ python ./B_question.py 5  < aaa | ./msort_3 > aaa
B_question: Q.5 Exp:ABEDC
B_question: Query 1: A < B
B_question: Query 2: C > D
B_question: Query 3: A < D
B_question: Query 4: B < D

ここまでで4個のソートが完了。最後にEの場所を二分探索で求める。

B_question: Query 5: D > E
B_question: Query 6: B < E
B_question: Ans ABEDC
B_question: Accepted !!  (count=6)

このケースはたった6回で終わりました。
一見、これで全てうまくいくかと思いましたが、うまくいかないパターンもあります。

例えば、AECBD(15番目のテストサンプル)の場合です。

$ python ./B_question.py 15  < aaa | ./msort_3 > aaa
B_question: Q.15 Exp:AECBD
B_question: Query 1: A < B
B_question: Query 2: C < D
B_question: Query 3: A < C 
B_question: Query 4: B > C
B_question: Query 5: B < D

ここまでで4個のソートが完了。最後にEの場所を二分探索で求める。

B_question: Query 6: B > E
B_question: Query 7: C > E
B_question: Query 8: A < E
B_question: Ans AECBD
B_question: Query count over... count= 8

７回を超過してしまいます。
なお、二分探索でACBDのBを起点としていますが、仮にCを起点とすればこのケースは1回減ります。ただ、別のケース(B<Eの場合)の回数が増えるので、同じことです。

冗長な箇所を分析

この手順で冗長なところを見てみます。

$ python ./B_question.py 15  < aaa | ./msort_3 > aaa
B_question: Q.15 Exp:AECBD
B_question: Query 1: A < B
B_question: Query 2: C < D
B_question: Query 3: A < C

ここまでは、特に冗長な点はありません。
ここまでで、A<B, A<C<D と判明します。

B_question: Query 4: B > C
B_question: Query 5: B < D

この二つの手順は、ACDの3個に対してBの場所を二分探索で求めているとも言えますが、既にBはAより大きいことが分かっているので、実際はCDの2個に対して二分探索しています。結果、2回も比較が必要となる場合があり、ちょっともったいないです。
（仮にBとAを比較してない場合、ACDの3個から二分探索で求めるのも2回の比較で済む）

マージソートのやり方では、4個のみで一旦ソートしようとするためですが、実際は5個目が残っているので後回しでもよいのかもしれません。3個と2個に分割したときも同様の話がありました。

B_question: Query 6: B > E
B_question: Query 7: C > E
B_question: Query 8: A < E
B_question: Ans AECBD
B_question: Query count over... count= 8

最後の手順は、Eの場所を求めるためにACBDの4個に対して二分探索します。結果、3回も比較が必要となる場合があります。最後の1個がここまで1回も比較をしておらず情報がないため、そうなっていると思われます。

処理順序変更 (AC)

更にいろいろ試行錯誤しましたが、結論から言うと、上の手順の処理順序を入れ替えてやるとうまくいきました。

4個だけのソートを完了させる前に、5番目を二分探索でマージし、その後に保留にしていたマージを再開するようなイメージです。

実行結果は以下の通りです。

$ python ./B_question.py 15  < aaa | ./B_msort_accepted > aaa
B_question: Q.15 Exp:AECBD
B_question: Query 1: A < B
B_question: Query 2: C < D
B_question: Query 3: A < C

4個のソートの途中です。ここまで3回の比較で A<B, A<C<D と判明します。

B_question: Query 4: C > E
B_question: Query 5: A < E

次にACDの3個に対してEの場所を二分探索で求めます。比較はせいぜい2回で済みます。

B_question: Query 6: C < B
B_question: Query 7: D > B
B_question: Ans AECBD
B_question: Accepted !!  (count=7)

最後にECDの3個に対してBの場所を二分探索で求めます。比較はせいぜい2回で済みます。

そうです！ この手順でやれば、120通りの全てのテストケースについて比較回数を7回以内に抑えることに成功しました！

こちらのシェルスクリプトで全パターンを一気にチェックできます。

$ cat all.sh 
#!/bin/sh
a=0
while [ $a -lt 120 ]
do
    #echo $a
    python ./B_question.py $a -s < aaa | $1 > aaa
    a=`expr $a + 1`
done

実行結果はこんな感じです。

$ ./all.sh ./B_msort_accepted 
B_question: Q.0 ABCDE Accepted !!  (count=7)
B_question: Q.1 ABCED Accepted !!  (count=7)
B_question: Q.2 ABDCE Accepted !!  (count=7)
B_question: Q.3 ABECD Accepted !!  (count=7)
B_question: Q.4 ABDEC Accepted !!  (count=7)
B_question: Q.5 ABEDC Accepted !!  (count=7)
 :

B_question: Q.116 DCEBA Accepted !!  (count=7)
B_question: Q.117 ECDBA Accepted !!  (count=6)
B_question: Q.118 DECBA Accepted !!  (count=7)
B_question: Q.119 EDCBA Accepted !!  (count=6)

ソースは以下に置いてあります。

AtCoder/PracticeContest at master · picomikan/AtCoder
Contribute to picomikan/AtCoder development by creating an account on GitHub.
github.com
スポンサーリンク

まとめ

今回、AtCoderの B – Interactive Sortingを試行錯誤の末、なんとか解くことができましたので、まとめてみました。行き当たりばったりでしたし、もっと分かりやすい導き方があるのかもしれません。もし分かったら、アップデートしていきたいと思います。

それにしても、practice contest(練習問題)でいきなりこんな超難問が出るなんて、ハードル高いですね。。もしやアルゴリズムとか数学界では常識問題？ 私ももっと勉強しなきゃですね。(^^;;

 

最後までお読みいただきありがとうございました！

スポンサーリンク
タイトルとURLをコピーしました